
Una piedra para vestir al infinito

Agustín B. Ávila Casanueva*
Hay muchos infinitos. Cada uno con su tema y su definición. Hay unos pequeños y otros grandes. Algunos sencillos y otros bastante complicados. El infinito que habita un plano de es bastante caprichoso. Y la verdad es que no es para menos. La gente que estudia matemáticas lleva cientos de años discutiendo cómo es que se puede vestir a este plano infinito.
Hay respuestas obvias. Los cuadrados, triángulos equiláteros y hexágonos regulares logran hacer el trabajo de manera simple. Son capaces de teselar un plano infinito, es decir, cubrirlo por completo sin dejar espacios ni superponer las figuras. Pero, de nuevo, nuestro infinito es caprichoso, no le gusta tener diseños simples y mucho menos, repetibles. Disfruta ser un ícono de la moda y dar de qué hablar. Antes muerto que sencillo. O dicho con mayor precisión matemática: antes muerto que periódico. Pero ¿a qué se refiere este infinito con tener un patrón periódico? Sabemos que un patrón es periódico cuando podemos repetirlo y continuar cubriendo el plano simplemente desplazando sus componentes hasta la siguiente sección a cubrir, como pasaría con un conjunto de cuadrados o hexágonos. Las periodicidades también se mantienen si las rotaciones repiten el patrón. Por ejemplo, si rotamos un patrón de cuadrados, cada 90° repetiríamos el patrón, y después de cuatro rotaciones de 90° volveríamos al acomodo original, por lo tanto, se dice que tiene una simetría rotacional de cuarto orden.
Los sastres matemáticos, por fortuna, han logrado darle unas cuantas opciones para poder cubrir toda la extensión del plano de manera aperiódica, repitiendo tan solo unas cuantas piezas, pero cuyas restricciones geométricas hacen que cada acomodo sea único e irrepetible, justo como le gusta a nuestro infinito. El primer ejemplo lo consiguió Robert Berger en 1964. No era muy práctico, la verdad, pero si uno tenía una paciencia infinita para acomodar 20,426 piezas distintas, se lograban armar patrones irrepetibles.
Con algo de talacha y bastante imaginación, las piezas involucradas se fueron reduciendo. En 1971, Raphael Robinson logró reducir a solamente seis el número de piezas o mosaicos necesarios para teselar el plano de manera aperiódica. Nuestro infinito estaba mucho más contento. En esa misma década, Roger Penrose encontró dos mosaicos que lograban hacer el truco. Y con esto, quedó abierto un gran reto ¿existiría alguna figura que permitiera cubrir todo el plano sin que se generara ninguna simetría? El goce máximo de nuestro infinito, una cobertura única, sin igual, pero elegantemente construida. Este se empezó a conocer como el problema einstein, lo cual es un juego de palabras entre el apellido del físico al que le gustaba sacar la lengua en las fotos y las palabras alemanas para decir una piedra, “ein stein”.
Justamente el lunes pasado nuestro infinito se despertó con la noticia de que cuatro sastres matemáticos habían encontrado un mosaico, una sola piedra con la que era posible vestir a todo el infinito del plano de manera aperiódica. David Smith, Joseph Samuel Myers, Craig S. Kaplan, y Chaim Goodman-Strauss publicaron en el repositorio arxiv math de la Universidad de Cornell, un artículo titulado “Un mosaico aperiódico”. Aunque en su artículo ofrecen dos posibles pruebas de que esta piedra, una pieza de mosaico de trece lados y que tiene la forma de una camisa o un sombrero, logra realmente cubrir el plano de manera aperiódica, el artículo no ha sido revisado aún por pares.
Una de las preguntas que más se le hace a la matemática es sobre su utilidad: Bueno, sí, pero ¿y eso para qué? Si bien los resultados de Penrose llevaron a investigaciones que le hicieron ganar el Premio Nobel de Química en el 2011 a Dan Shechtman, por fortuna para los autores de esta nuevo propuesta, la prensa científica y para nuestro infinito quisquilloso, el día siguiente a la publicación, el martes 21 de marzo, fue el Día Mundial de la Poesía, así que bastaba y sobraba con la promesa de haber encontrado una piedra capaz de vestir a un plano infinito sin repetir nunca su patrón.
*Coordinador de la Unidad de Divulgación del Centro de Ciencias Genómicas de la UNAM y miembro de la Red Mexicana de Periodistas de Ciencia.
Agradezco a la Dra. Vanessa Alderete el revisar el uso de los conceptos matemáticos en esta columna. Cualquier acierto corresponde a su labor, cualquier falta a mi torpeza.

Una muestra de la teselación del plano con un único mosaico. El patrón nunca se repite. Imagen tomada del artículo subido a la plataforma arxiv math.
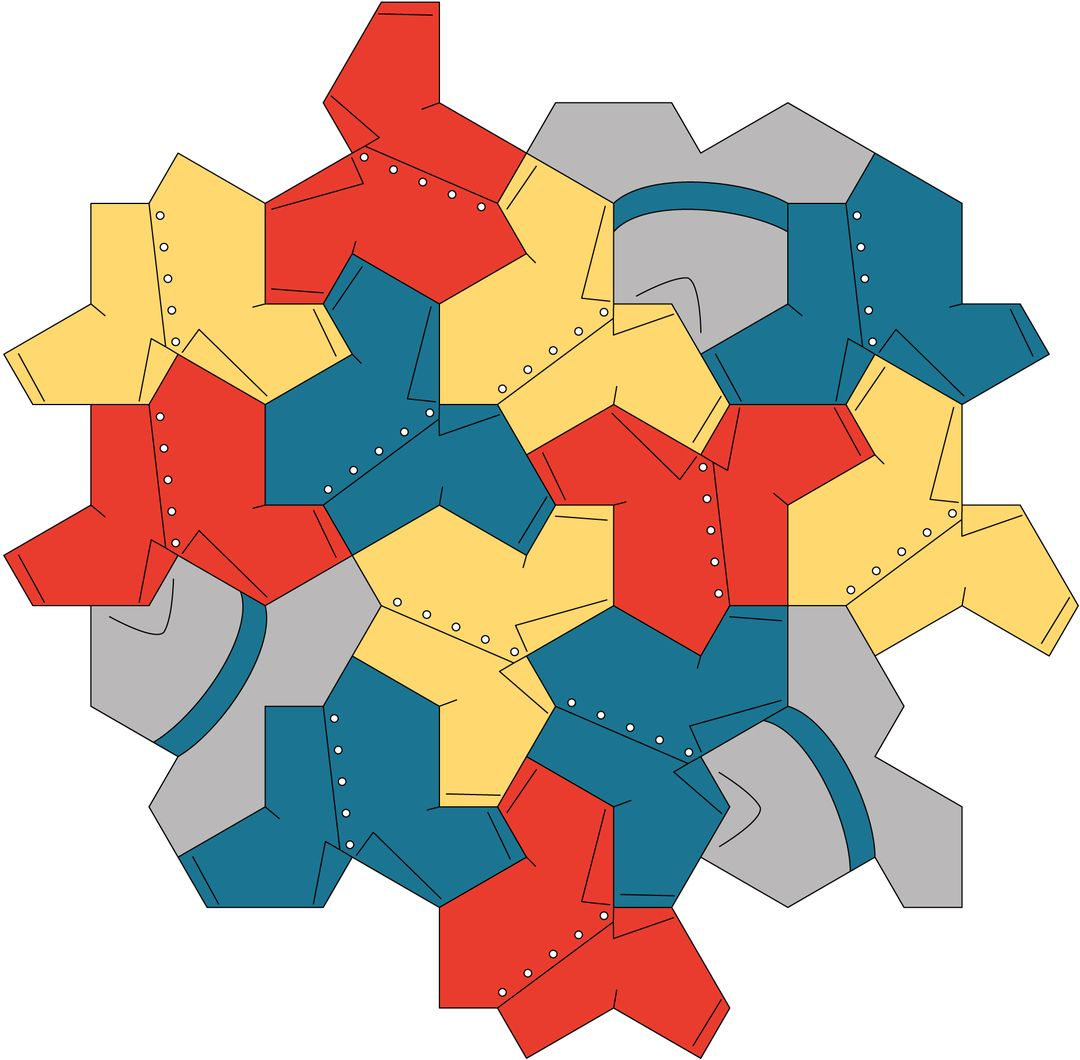
El mismo mosaico, pero ilustrado como camisa y sombrero. Imagen: Robert Fathauer Art.







